

2009-1-29: Practice exercise for the day:
A vector V=(3; 4) (originates at the origin). Find the point that lies 55 units in the direction of the vector V.
SOLUTION: First normalize the vector V. |V|=sqrt(3^2+4^2)=5. N=[3/4; 4/5]. Multiply the normalized vector by 55 to find the solution: N*55 = [3*55/5; 4*55/5] = [33;44]
Dot product discussion, it is important to understand the geometric interpretation of the dot product as a projection operation. In other words, given a unit length vector N, taking the dot product of any point P with N projects P onto an axis (direction) defined by N ... and this in turn is a means of measuring the distance of P from the origin in the direction defined by N.




Here are several of the key elements of this slide explained
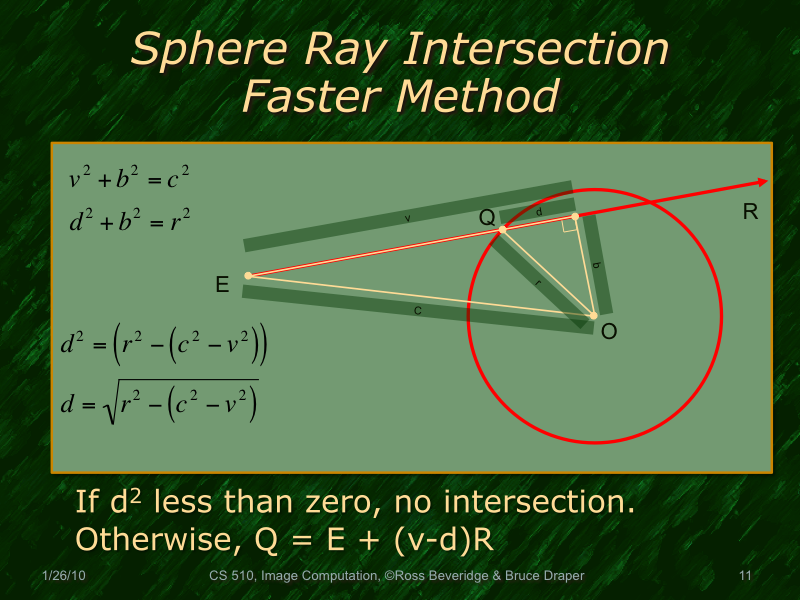
- P is any point on the sphere and the equation of our ray is substituted in place of P in the first step - first to second equation.
- L is a 3D point on the image plane that serves as the base of the ray and Pc is the center of the sphere. Both of these are knowns (constant), so to simplify the equation the vector from L to Pc is named T and used in the resulting quadratic equation.


















At this point in the lecture we spent time reviewing how to derived the implicit form for a 2D line based upon two points known to lie on the line, and then how to use the implicit form to determine whether a third point is above the line, below the line, or exactly on the line. A more detailed description can be found in the CS 410 lecture notes, slides 15, 16 and 17.
The methods:
- Odd/Even Parity: create a ray from the intersection point to any direction in the same polygon plane then count the # of intersections with edges (a vertex is count as 1 intersection). if the # is even (including 0) --> the point is outside the polygon (because it is either 0 intersections which means it is definetly outside, or it will need at least 2 intersections to get inside and out again), otherwise (odd) --> the point is inside the polygon.
- draw lines from the point to the vertices then sum the angles between these lines. If the sum = 360 --> the point is inside. (second figure)
- By knowing the normals of the polygon edges (3rd figure) we can know if the point is inside or outside the polygon: An edge is represented by the following equation (ax + by + c = 0). a, b , and c are calculated by knowing the edge end points. Then we can substitute x and y by the point coordinates. If the result is 0 --> the point is on the edge. If result > 0 --> the point is at the edge normal side. If result < 0 --> the point is at the side oppisite of the edge normal.





An inefficient way: is to project the polygon plane on one of the xyz planes according to the face normal: the axis that is closest to this normal is avoided, so the face is projected on the plane defined by the other 2 axises.




Dan Sunday has written Intersections of Rays, Segments, Planes and Triangles in 3D. In this short piece is a concise description of a very efficient algorithm for intersecting a ray with a triangle. We will go over this algorithm in detail in lecture.
Some notes on this page:
- V(s,t) equation is used to describe the points in the triangle {V0,V1,V2}, where s is in [0,1] and t is in [0,1].
But V(1,1) is a point outside the triangle (it will result in the 4th vertex if we complete the triangle to be Parallelogram "move from V0 1 unit in the direction V0→V1 then 1 unit in the direction V0→V2"). So we need constraints on s & t → (s + t <=1).
- A beautiful implication of this is that, by removing the "(s + t <=1)" check, the exact same code should work for insideness checks on parallelograms (think checkerboards). Hmmm...or maybe just rectangles?
(s+t=1 defines the line {V1,V2})
But when s or t or both are negative → point is outside the triangle. So we need more constraints: (s >= 0) and (t >= 0).
- u and v should not be normalized because t should be in the range from 0 to 1 regardless of the units used underline.


Let's try using this space as a common place for questions, suggestions and clarifications on Project 1.
Ross (1/27/10)
One of the criteria mentioned in the assignment is that we are to "provide a mechanism for specifying an external scene model". The word "external" seems to mean that we should be reading from a source external to the program (i.e., the scene should not be hardcoded). I'm assuming based upon your comments in class (err...last Wednesday?) that this requirement is at least relaxed (i.e., maybe we get more credit for reading the defn. from a file) or dropped altogether. Is that correct?
Erik (1/30/10)
Erik is correct that I relaxed the criteria for an external scene model. Your ray tracers must provide three distinct scenes as described in the project assignment. I also think you may find it very helpful to define a simple means of controlling the contents of the scene through some external specification. However, it is not going to be formally required - if you choose you can generate scenes entirely from within your code.
Ross (1/30/10 8:20PM)
When calculating the light (diffuse and specular) that is hitting a given intersection point on a surface, shouldn't we consider whether or not the light sources are obscured by other objects? The slides discussing lighting don't seem to consider this case (or I'm not seeing something obvious...).
Alan (2010/2/5 13:10)

Colorado State University, Fort Collins, CO 80523 USA
© 2010 Colorado State University



