When you design an experiment, consider the following items:
The Experimental Procedure Often, the experiment is so simple that you'll assume you understand the procedure, but making it explicit helps to find spurious effects and sampling biases.
An Example of a Data Table Lay out your data table with independent and dependent variables in columns. This shows you what is being varied and what data are being collected. Now consider the rows. How often will data be collected? At the end of each trial? At regular intervals? After significant events? Do you need a variable to time-stamp your data? If you can put hypothetical numbers in the table, so much the better, because then you can consider an example of your analysis.
An Example of Your Analysis A common complaint from statistical consultants is that their clients collect reams of data with only a vague notion of how it will be analyzed. If you think through the analysis before running the experiment, you can avoid collecting too much or too little data and you often can find a better experiment design. These benefits are especially likely when your experiment is intended to find interaction effects, because these experiments inherently involve combinations of conditions, which complicate analysis and confuse humans.
A Discussion of Possible Results and Their Interpretations
What do potential results mean? It is very helpful, especially in complex
designs, to sketch hypothetical results and see how you would explain
them. Consider, for instance, a factorial experiment with two
independent variables, 
and 
, and a continuous
dependent variable y. You plan to calculate the mean of y in
each of four conditions defined by the combination of two values of
each of and . A useful trick is to plot some possible
outcomes and see whether you can interpret the results, as shown in
Figure 3.12. In case A, clearly has an effect
on y because mean y values are higher at 
than at
at both levels of . Similarly, mean y values are
higher at 
than at 
`, irrespective of the values
of . In case A, and have
independent effects on y. In contrast, in cases B and C, the
effect of on y depends on the value of or vice
versa. Your interpretation of cases B and C might be that the
influence of on y is controlled or ``gated'' by .
The point is that sketches like Figure 3.12 help you
consider the possible outcomes of your experiment, often raising
possibilities that you wouldn't have considered otherwise, and help to
determine whether the experiment design can actually produce the
results you are looking for.
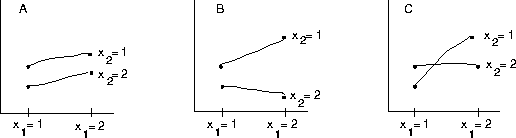
Figure 3.12 Rough sketch of potential outcomes of a two-factor experiment.
Now, what was the question, again? Experiment design is a seductive activity, made more so by easy statistical analysis. You can design an experiment and an analysis that do not actually answer the question you initially asked. You should double check the potential results against the question. Do they answers the question? Nothing prevents you from changing the question if, while designing the experiment, you find one you'd rather answer, or one that better summarizes your research interest. Still, check whether the experiment answers your question.