Dependency detection is syntactic and requires little knowledge of the planner or its environment; thus, it can be applied to any planner in any environment. To begin, we gather execution traces of the planner. To determine how the planner's actions might lead to failure, the execution traces include failures and the recovery actions that repaired them, as in the following short trace:
F's are failures (e.g., 
is the
Insufficient Progress failure in Phoenix) and R's are recovery
actions (e.g., 
is the Substitute Projection action in the
Phoenix Planner's recovery action set). It appears from this short
trace that the failure ip is always preceded by the recovery
action sp. We call disproportionately high co-occurrences
between failures and particular precursors dependencies. In this
example, the precursor of ip is the action sp, but
conceptually, it could be any combination of predecessors in the
trace: the preceding failure, the combination of the failure and the
recovery action that repaired it, or even longer combinations of
previous actions and failures. Currently, the analysis looks at only
singles (i.e., failures or recovery actions) and pairs (i.e., failures
and recovery actions) as precursors.
With more data, we can test whether the observed relationship between
sp and ip is statistically significant. We build a contingency table
of four cells: one for each combination of precursor and failure and
their negations. For example, the contingency table in Table 1 tests
whether depends on the precursor .
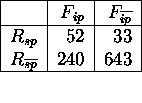
Table 1: Contingency table for testing the pattern 
.
We test the significance of the observed relationship, , with a G-test on the contingency table. A G-test
on this table is highly significant, G=42.86,p=.001, meaning that it
is highly unlikely that the observed dependence is due to chance or
noise.
We construct contingency tables for three types of immediate
precursors: failures, recovery actions, and a combination of a failure
and the recovery action that repaired it. We denote these cases 
, 
, and 
,
respectively. The three types overlap. In particular, is a special case of both and
(because they subsume all possible values of the missing member), so
if the former dependency is significant, we do not know whether it is
truly a dependency between a 
and the subsequent 
, or
between 
irrespective of the intervening action, or between R
with the initial failure playing no role. In practice, all three
dependencies might be present to varying degrees.
We sort out the strengths of the dependencies by running a variant on
the G-test called the Heterogeneity G-test [Sokal and Rohlf 81]. The
intuition is that we compare the contributions of subsets to that of
the superset; one can imagine looking at a Venn diagram (as in
Figure 1) to gauge whether the failure ner, the
recovery action sp or the combination seems to account for most
of the area in the intersection with the subsequent failure
ip. Both 
and overlap with part of the subsequent
, but it is easy to see that a larger proportion of
than overlaps with . Thus, is a more
reliable precursor for .
Figure did not convert
Figure 1: Venn diagram representing the data for the precursors and the
following failure.
Similarly, but somewhat harder to see, the proportion of
(the darker shaded area plus the cross hatched area)
that overlaps with (just the darker shaded area) is about the
same as the proportion of (the area in the heavy box) that overlaps
with (the two shaded areas), suggesting that we can generalize the
relationship without loss of information. To compute the overlap, we
add the G values for each of the subsets together (e.g., for , we add G values for all possible R's) and compare the
result to the G value for the superset; if the difference is
significant, then the subsets account for more of the variance in the
dependency and so cannot be generalized. For this example, the G
values for the subsets add to 45.89; the difference between that and G
for the superset is 3.035, which is not a significant
difference at the .05 level.